Solving Problems Using Dimensional Analysis - Clinical Calculations Made Easy: Solving Problems Using Dimensional Analysis, 3rd Edition

Clinical Calculations Made Easy: Solving Problems Using Dimensional Analysis, 3rd Edition

Chapter 3.Solving Problems Using Dimensional Analysis

Objectives

After completing this chapter, you will be able to:

1. Define the terms used in dimensional analysis.

2. Explain the step-by-step problem-solving method of dimensional analysis.

3. Solve problems involving common equivalents using dimensional analysis as a problem-solving method.

TERMS USED IN DIMENSIONAL ANALYSIS

Dimensional analysis is a problem-solving method that can be used whenever two quantities are directly proportional to each other and one quantity must be converted to the other by using a common equivalent, conversion factor, or conversion relation. All medication dosage calculation problems can be solved by dimensional analysis.

It is important to understand the following four terms that provide the basis for dimensional analysis.

· Given quantity: the beginning point of the problem

· Wanted quantity: the answer to the problem

· Unit path: the series of conversions necessary to achieve the answer to the problem

· Conversion factors: equivalents necessary to convert between systems of measurement and to allow unwanted units to be canceled from the problem

Each conversion factor is a ratio of units that equals 1.

Dimensional analysis also uses the same terms as fractions: nume rators and denominators.

· Numerator = the top portion of the problem

· Denominator = the bottom portion of the problem

Some problems will have a given quantity and a wanted quantity that contain only numerators. Other problems will have a given quantity and a wanted quantity that contain both a numerator and a denominator. This chapter contains only problems with numerators as the given quantity and the wanted quantity.

Once the beginning point in the problem is identified, then a series of conversions necessary to achieve the answer is established that leads to the problem's solution.

Below is an example of the problem-solving method, showing the placement of basic terms used in dimensional analysis.

Figure. No caption available

THE FIVE STEPS OF DIMENSIONAL ANALYSIS

Once the given quantity is identified, the unit path leading to the wanted quantity is established. The problem-solving method of dimensional analysis uses the following five steps.

1. Identify the given quantity in the problem.

2. Identify the wanted quantity in the problem.

3. Establish the unit path from the given quantity to the wanted quantity using equivalents as conversion factors.

4. Set up the conversion factors to permit cancellation of unwanted units. Carefully choose each conversion factor and ensure that it is correctly placed in the numerator or denominator portion of the problem to allow the unwanted units to be canceled from the problem.

5. Multiply the numerators, multiply the denominators, and divide the product of the numerators by the product of the denominators to provide the numerical value of the wanted quantity.

The following examples use the five steps to solve problems using dimensional analysis.

EXAMPLE 3.1

EXAMPLE 3.2

Exercise 3.1 Dimensional Analysis (See pages 53–54 for answers)

Use dimensional analysis to change the following units of measurement.

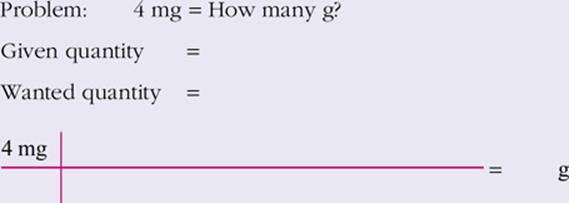
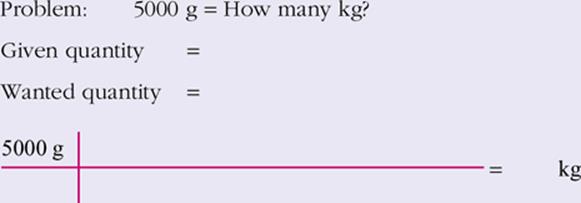
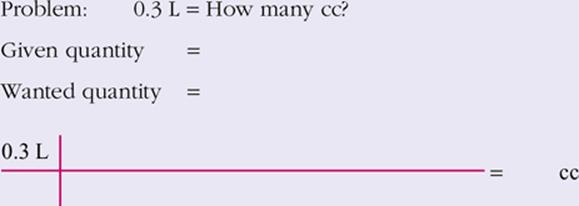
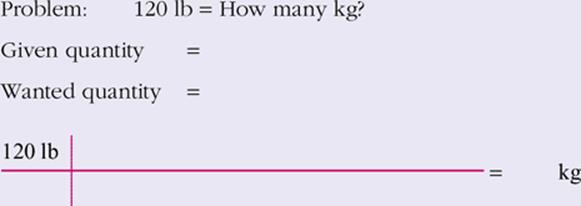
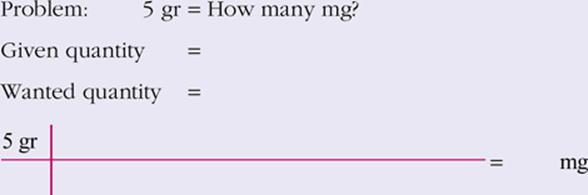
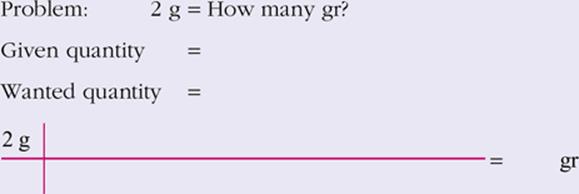
View Answer

10.

View Answer

11.

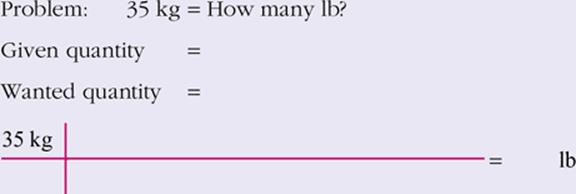
View Answer

12.

View Answer

13.

View Answer

14.

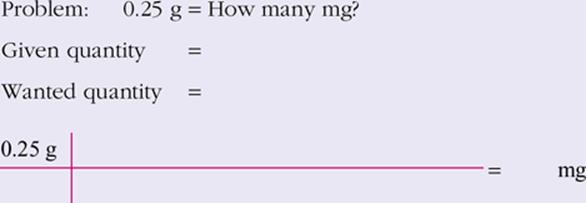
View Answer

15.

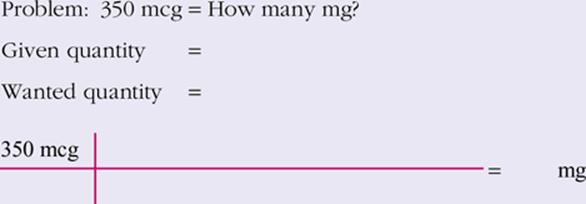
View Answer

16.

View Answer

17.

View Answer

18.

View Answer

19.

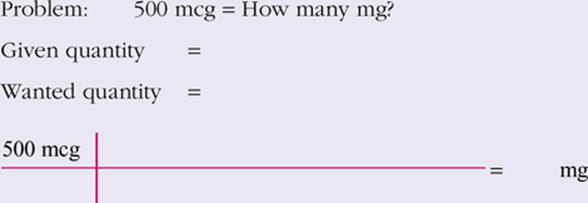
View Answer

20.

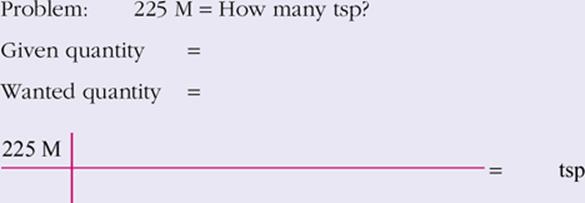
View Answer

SUMMARY

This chapter has introduced you to dimensional analysis with a step-by-step explanation and an opportunity to practice solving problems involving common equivalents. To demonstrate your understanding of dimensional analysis and conversions between systems of measurement, complete the following practice problems.

Practice Problems for Chapter 3: Solving Problems Using Dimensional Analysis (See pages 55–56 for answers)